앞선 내용에서 data로부터 parameter를 estimation하는 방법을 배웠지만, 대체로 point estimate을 구하는 내용이었다.
point estimate을 구하면 estimation에 대한 uncertainty를 모델링하기 위한 방법이 없고, 이를 위해 좋은 방법이 Bayesian statistics 를 이용하는 것이다.
통계학에서, 파라미터에 대한 불확실성을 확률분포를 이용하여 모델링 하는 방식을 Infernece 라고 한다.
헷갈리지 말아야 할 게, 딥러닝을 하는 사람들 사이에서는 학습된 모델의 파라미터를 이용해서 testing을 진행하는 것을 inference라고 하기도 한다.
Bayesian에서는 불확실성을 모델링하기 위해 posterior distribution 을 이용한다. 이를 위해선 두 가지가 필요하다.
Prior \( p(\boldsymbol{\theta}) \): 데이터를 보기 전 파라미터에 대한 probability distribution
Likelihood \( p(\mathcal{D}|\boldsymbol{\theta}) \): 주어진 parameter에 대해 observation이 얼마나 likely한지
Bayesian inference를 위한 정확한 식은 아래와 같다.
\[p(\boldsymbol{\theta}|\mathcal{D}) = \frac{p(\boldsymbol{\theta})p(\mathcal{D}|\boldsymbol{\theta})}{p(\mathcal{D})} \qquad{(4.112)}\]
여기서 분모의 \( p(\mathcal{D}) \)는 데이터에 대한 marginal likelihood 라고 한다. unknown \( \boldsymbol{\theta} \)값에 대한 부분을 marginalize out 했기 때문이다.
다만 \( \boldsymbol{\theta} \)에 대한 식이 아니기 때문에 prior * likelihood 텀만 고려하는 경우가 대부분이다.
추가로, marginal likelihood는 많은 경우에 analytic하게 계산할 수 없다.
여기서 data \( p(\mathcal{D}) \)는 주어지는 setting에 따라 크게 두가지로 나뉘는데,
Supervised learning의 경우 \( \mathcal{D} = { (\mathbf{x}_n, \mathbf{y}_n): n = 1:N } \)와 같이 data pair가 주어지고
Unsupervised learning의 경우 \( \mathcal{D} = {\mathbf{y}_n): n = 1:N} \)와 같이 단순히 데이터만 주어진다.
Posterior를 계산하고 나서는 다음에 올 observation에 대해 Bayes model averaging(BMA) 를 통해 parameter 값을 marginalize out해서 값을 예측 가능하다.
이를 posterior predictive distribution 이라고 한다.
Supervised case:
\[p(\mathbf{y}|\mathbf{x}, \mathcal{D}) = \int p(\mathbf{y}|\mathbf{x}, \boldsymbol{\theta})p(\boldsymbol{\theta}|\mathcal{D}) d\boldsymbol{\theta} \qquad{(4.113)}\]
\[p(\mathbf{y}|\mathcal{D}) = \int p(\mathbf{y}|\boldsymbol{\theta})p(\boldsymbol{\theta}|\mathcal{D}) d\boldsymbol{\theta}\]
결국, 가능한 모든 parameter value \( \boldsymbol{\theta} \)에 대한 prediction을 average하는 것으로 해석할 수 있다.
1. Conjugate priors
이 섹션에서는 posterior를 closed-form으로 표현하기 위한 (prior, likelihood) pair를 몇 가지 알아본다.
이어지는 섹션들에서는 더 표현이 간단한 Unsupervised case에 집중한다.
prior가 likelihood에 대해 conjugate 이라는 말은 posterior가 prior과 동일한 함수의 형태 를 띈다는 말이다.
많은 경우에, prior과 likelihood가 exponential family의 일종이면 closed-form computation이 가능하다.
2. The beta-binomial model
동전을 N번 던지는 경우를 가정하자.
\( y_n = 1 \): Head
\( y_n = 0 \): Tail
\( \mathcal{D} = { y_n : n = 1 : N } \): Dataset
\( y_n \sim \textrm{Ber}(\theta) \)
2.1 Likelihood
iid 가정 하에 Likelihood는 아래와 같이 표현된다.
\(N_1, N_0 \): Number of heads, tails
\(N = N_1 + N_0\): Total count, dataset size
\[p(\mathcal{D}|\theta) = \prod_{n=1}^{N} \theta^{y_n}(1-\theta)^{1 - y_n} = \theta^{N_1}(1 - \theta)^{N_0} \qquad{(4.114)}\]
이 경우 \(N_1, N_0 \)이 distribution에 대해 모든 것을 말해주기 때문에 이를 sufficient statistics 라고 한다.
Bernoulli trial을 N번 반복하는 것이 아니라, 전체 N번이 있고 이 중 몇번의 head가 나왔는지로 해석할 수도 있다. 이 경우엔
\[p(\mathcal{D}|\theta) = \begin{pmatrix}N\\y\end{pmatrix}\theta^{y}(1 - \theta)^{N-y} \qquad{(4.114)}\]
결국 coefficient를 무시하면 같은 결과를 얻는다.
2.2 Prior
Likelihood에 대한 conjugate prior 를 구하고 싶기 때문에, Bernoulli/Binomial에 대해 conjugate인 distribution을 고려하자. Functional form을 생각해보면 아래와 같이
Beta distribution 으로 정하는 것이 합리적이다.
\[p(\theta) \propto \theta^{\breve{\alpha} - 1}(1 - \theta)^{\breve{\beta} - 1} \qquad{(4.116)}\]
2.3 Posterior
위에서 가정한 Bernoulli likelihood와 Beta prior의 product인 posterior distribution을 구해보자.
\[\begin{align}
p(\theta|\mathcal{D}) &\propto \theta^{N_1}(1 - \theta)^{N_0}\theta^{\breve{\alpha} - 1}(1 - \theta)^{\breve{\beta} - 1}\\
&\propto \textrm{Beta}(\theta|\breve{\alpha} + N_1, \breve{\beta} + N_0)\\
&= \Beta(\theta|\hat{alpha}, \hat{\beta})
\end{align}\]
여기서 notation의 편의성을 위해
\( \hat{alpha} = \breve{\alpha} + N_1 \)
\( \hat{beta} = \breve{\beta} + N_0 \) 를 정의했다.
Prior distribution의 파라미터는 data의 observation과 무관하게 설정하고 시작하기 때문에 hyper-parameter 라고 한다.
Deep learning에서도 gradient descent를 통해서 학습하는 parameter가 아닌 학습을 위해 사전에 정의하고 가는 파라미터들을 하이퍼파라미터로 칭한다.
Beta-binomial 모델의 경우 사전에 정의한 하이퍼파라미터 \( \breve{\alpha}, \breve{\beta} \)가 head/tail의 count 역할을 한다는 것은 자명하다.
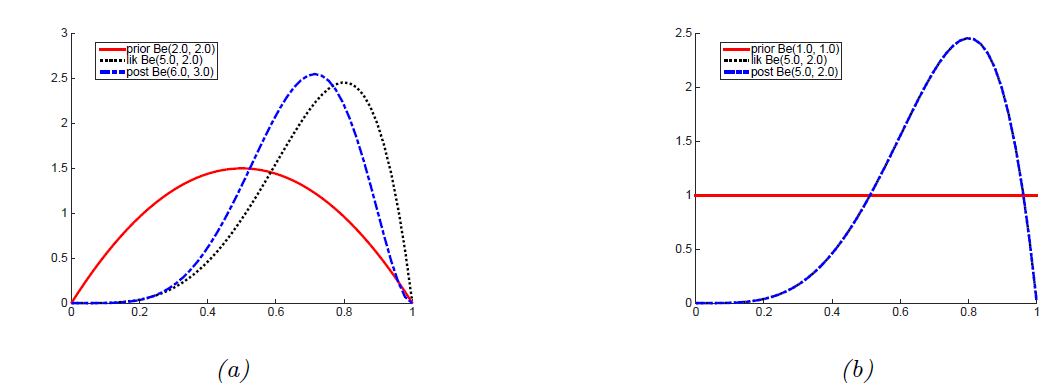
위 그림 (a)처럼, \( \breve{\alpha} = \breve{\beta} = 2 \) 로 prior를 정한 경우를 생각해보자.
각 파라미터가 head, tail의 count와 관련이 있기 때문에, prior를 이렇게 정하는 것은 결국 probability = 0.5 에 대한 weak preference라고 할 수 있다. (그림에서도 pdf를 확인 가능하다.)
이 경우 Likelihood가 (a)의 회색 plot일 때, posterior는 prior과 likelihood 사이의 어딘가인 파란색 plot으로 귀결된다.
만약 \( \breve{\alpha} = \breve{\beta} = 1 \)로 정의하면, 이는 uniform distribution과 equivalent해서 uninformative prior 에 해당한다.
이는 그림 (b)에 해당하는 부분으로, likelihood와 posterior가 정확히 일치하는 것을 확인할 수 있다.
Posterior distribution \( p(\theta|\mathcal{D}) \)자체가 prior/observation을 summarize해주는 역할을 해주기는 하지만, 이보다 더 간단하게 point esitmate 로도 summarize가 가능하다.
예컨대, posterior mean, posterior variance와 같이 distribution을 summarize할 수 있는 statistical value들이다.
\( \hat{N} = \hat{\alpha} + \hat{\beta} \)로 정의할 때, posterior mean은
\[\bar{\theta} := \mathbb{E}[\theta|\mathcal{D}] = \frac{\hat{\alpha}}{\hat{\alpha} + \hat{\beta}} = \frac{\hat{\alpha}}{\hat{N}} \qquad{(4.121)}\]
위와 같은 posterior mean은, (직관적인 해석과도 일치하게) prior mean과 MLE의 convex combination 이다. 아래를 정의하면 이를 확인할 수 있다.
\( m = \breve{alpha} / \breve{N} \): prior mean
\( \breve{N} := \breve{\alpha} + \breve{\beta})\): prior strength
\( \hat{\theta}_{mle} \) = N_1 / N: MLE
\( \lambda = \breve{N} / \hat{N} \): prior 대 posterior sample size 크기
\[\mathbb{V}[\theta|\mathcal{D}] = \frac{\breve{\alpha} + N_1}{\breve{alpha} + N_1 + \breve{\beta} + N_0} = \frac{\breve{N}m + N_1}{N + \breve{N}}
= \frac{\breve{N}}{N + \breve{N}}m + \frac{N}{N + \breve{N}}\frac{N_1}{N} = \lambda m + (1 - \lambda)\hat{\theta}_{mle}\]
또한, posterior(beta distribution)의 variance는 아래와 같이 정의된다.
\( \hat{\alpha} = \breve{\alpha} + N_1 \)
\( \hat{\beta} = \breve{\beta} + N_0 \)
\[\mathbb{V}[\theta|\mathcal{D}] = \frac{\hat{\alpha}\hat{\beta}}{(\hat{\alpha} + \hat{\beta})^2(\hat{\alpha} + \hat{\beta} + 1)} \qquad{(4.124)}\]
여기서, \( N » \breve{\alpha} + \breve{\beta} \) 라는 가정 하에, (대부분의 case로 볼 수 있다.)
\[\mathbb{V}[\theta|\mathcal{D}] = \frac{N_1 N_0}{N^3} = \frac{\hat{\theta}(1 - \hat{\theta})}{N} \qquad{(4.125)}\]
두가지 observation이 가능하다.
uncertainty는 \( 1/\sqrt{N} \)에 따라 감소한다.
uncertainty는 0.5에서 maximize된다.
직관적으로 생각해도, coin toss가 bias되어있다는데에 대한 확신을 갖는것이 공평하다는데에 대한 확신을 갖는것보다 쉽다.
Please enable JavaScript to view the comments powered by Disqus.
Please enable JavaScript to view the comments powered by Disqus.