3. Bayesian concept learning

지난 섹션에서는 hidden quantity \( h \in \mathcal{H} \) 를 단 하나의 observation \( y \) 로부터 유추하는 방법을 배웠다.
이를 일반화하면 observation이 하나가 아닌 여러 개로 이루어진 set 일 때를 생각할 수 있다. \( \mathcal{D} = { y_n : n = 1:N } \)
이제 목표는 주어진 데이터로부터 보편적인 특성(concept)을 찾는 일이다.
일반적으로 머신러닝을 통해 binary classification을 학습 시킬 때는 positive example과 negative example이 둘 다 충분히 많이 필요하다.
반면, 아이가 “강아지” 라는 컨셉을 처음 배울 때는 positive example만을 갖고도 효율적으로 학습한다.

1. Learning a discrete concept: the number game

우리가 어떤 수학적인 컨셉을 배운다고 가정하자. 편의를 위해 몇 가지 assumption이 필요하다.
- \( h_{even} = { 2, 4, 6, \dots } \) 와 같이 컨셉은 extension으로 설명된다.
- 숫자는 1부터 100 사이의 숫자이다.
\( \mathcal{D} = { 2, 8, 16, 64 } \) 가 주어지면, 많은 사람들이 일반적으로 이 set은 2의 승수로 이루어져있다고 판단할 것이다.
이는 generalization의 한 예시이며, \( \mathcal{D} = { 16 } \) 와 같이 데이터 하나만 주어졌을 때보다 데이터가 여러 개 주어졌을 때 더 정확히 일반화할 수 있고, underlying pattern 을 더 쉽게 찾을 수 있다.

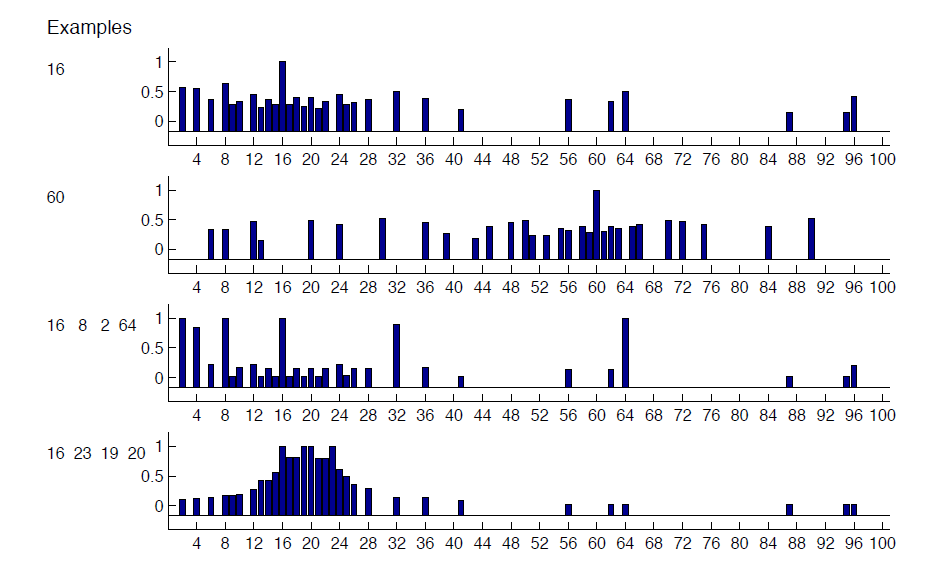
위 그림을 살펴보자. 첫 두 row에서 확인할 수 있듯이, 16과 60만을 본 뒤에는 다른 숫자를 고를 확률이 고르게 분포가 되어있지만, 4개의 숫자를 본 뒤에는 대체로 확률값들이 밀집되어 분포해있다.
이러한 induction problem을 수학적으로 설명하기 위해 hypothesis space \( \mathcal{H} \)가 있다고 가정한다.
- 짝수, 1과 10 사이의 모든 수 와 같은 것이 하나의 concept에 해당한다.
그 후, hypothesis space \( \mathcal{H} \) 에 존재하는 concept 중 observed data \( \mathcal{D} \)와 consistent하면서, 가장 크기가 작은 subset을 찾는다. 이를 version space 라고 칭한다.
그러나, version space theory를 이용해도 사람의 행동을 완전히 설명하기는 어렵다. 모든 짝수, 32를 제외한 모든 2의 승수 등의 subset도 모두 observation과 consistent하지만 사람들은능하다. 그러한 concept을 잘 제시하지 않는다. 이러한 현상 또한 bayesian inference로 설명이 가능하다.

1.1 Likelihood

왜 사람들은 \( \mathcal{D} = { 2, 8, 16, 64 } \) 를 보고 짝수가 아닌 2의 승수를 먼저 떠올릴까?
suspicious coincidences를 막기 위함이다. 실제 \( h \) 가 짝수였다면 왜 2의 승수만 관측됐을까?
이를 formal하게 표현하기 위해 observation(example)들이 concept의 extension으로부터 랜덤하게 샘플링 되었다고 생각해보자 (이를 strong sampling assumption이라 한다.)
이 때, unknown concept \( h \)로부터 아이템을 \( N \)개 sampling 하는 확률은 아래와 같다.

\[p(\mathcal{D}|h) = \prod_{n=1}^N p(y_n|h) = \prod_{n=1}^N \frac{1}{\textrm{size}(h)}\mathbb{I}(y_n \in h) = [\frac{1}{\textrm{size}(h)}]^N \mathbb{I}(\mathcal{D} \in h) \qquad{(2.16)}\]

observation의 모든 데이터 포인트가 \( h \)에 존재하여야 \( \mathbb{I}(\mathcal{D} \in h) \)가 0이 아닌 값을 가지며, 따라서 probability는 size가 작으면 작을수록 더 probable하다.
이를 size principle이라고 하고, Occam’s razor로 설명할 수도 있다.
\( \mathcal{D} = { 2, 8, 16, 64 } \) 일 때 \( h_{two} \) 일 확률은 \( (1/6)^4 7.7 \times 10 \) 인데에 비해, \( h_{even} \)일 확률은 \( (1/50)^4 = 1.6 \times 10^{-7} \) 에 불과하다.

1.2 Prior

Bayesian approach로 계산하려면 likelihood 뿐만이 아니라 각 hypothesis에 대한 믿음의 정도인 prior \( p(h) \)를 알아야 한다.
예컨대, \( \mathcal{D} = {16, 8, 2, 64} \)가 “32를 제외한 2의 승수”가 아니라 “2의 승수”에 해당하는 것이 더 가능성이 높다고 생각하는 데에는 그 이유를 prior에서 찾을 수 있다. Prior를 설정하는 데에는 어느 정도의 subjectivess가 포함될 수밖에 없다.
- 하지만 많은 경우에 prior는 “일반적으로 많은 사람들이 받아들일 수 있도록” 설정할 수 있으며, 위의 경우에는 “2의 승수”가 “32를 제외한 2의 승수”보다 훨씬 더 큰 prior probability를 가질 것이다.
- 이렇게 prior를 설정함으로써 (background knowledge를 끌어들임으로써) 빠른 학습이 가능해진다.
지금 이용하고 있는 예제에서는 hypothesis space를 30개로 제한한다.
1. Rule-like hypothesis
  - “even numbers”, “prime numbers”와 같이 term으로 정의할 수 있는경우
  - “powers of 2, plus 37”과 같이 직관적으로 unnatural한 term도 포함하고 다만 낮은 prior를 설정한다.
2. Interval hypothesis
  - \(a \) 이상 \( b \) 이하와 같이 특정 interval에도 어느정도의 prior value를 준다.

\[p(h) = \pi \textrm{Unif}(h|\textrm{rules}) + (1 - \pi)\textrm{Unif}(h|\textrm{intervals}) \qquad{(2.17)}\]

-합쳐서, 위와같은 mixture distribution을 정의할 수 있다.

1.3 Posterior

Likelihood과 prior를 설정했으니, posterior를 구할 수 있다.

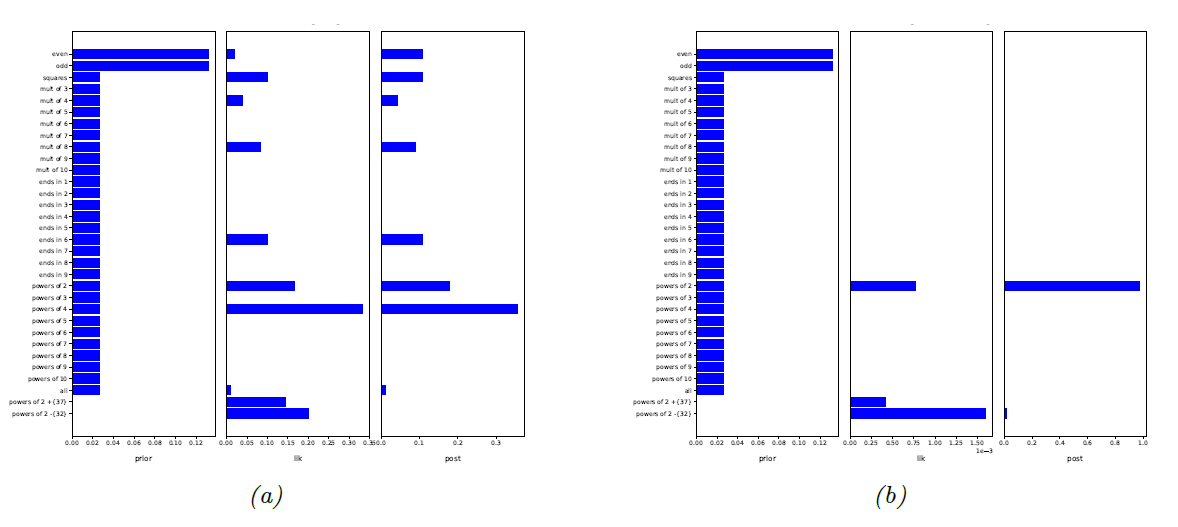
(a)는 \( \mathcal{D} = {16} \) 일 때의 prior/likelihood/posterior 값이고, (b)는 \( \mathcal{D} = { 2, 8, 16, 64 } \) 가 주어진 이후의 counterpart이다.
- prior가 hypothesis space를 많이 줄여주기는 하지만, (a)에서는 그래도 posterior에 다양한 hypothesis가 가능한 반면, (b)에서는 아주 작은 hypothesis space만이 남는다.
- 중요하게 확인할 수 있는 것은, “32를 제외한 2의 승수”와 같이 직관적으로 improable한 hypothesis들은 높은 likelihood값을 가지지만, prior 값이 작기 때문에 작은 posterior 값을 갖는다.
- 이 예시에서 왜 “32를 제외한 2의 승수”와 같이 unnatural한 컨셉에 low prior를 줘야 하는지를 알 수 있다. 만약 높은 prior를 줬다면 overfitting으로 posterior값이 가장 큰 hypotehsis는 “32를 제외한 2의 승수”가 되었을 것이다.

1.4 Posterior predictive

hypothesis에 대한 posterior는 우리의 belief state를 대변한다.
이러한 internal belief state를 시험할 수 있는 방법은 실측 가능한 값을 예측하는 것이다. (이는 scientific method의 근본이 된다.)
Posterior distribution을 가능한 hypothesis에 대해 marginalizing하는 방식으로 가능하며, 이를 posterior predictive distribution이라 칭한다.

\[p(y|\mathcal{D}) = \sum_h p(y|h)p(h|\mathcal{D}) \qquad{(2.18)}\]

위와 같은 방식으로 posterior predictive distribution을 구하는 방법을 Bayse model averaging이라고 한다.

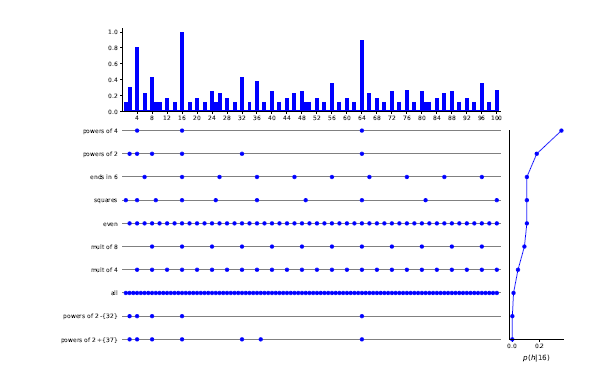
위 그림을 통해 이해해볼 수 있다.
- 점이 찍힌 각 row는 하나의 hypothesis에서의 prediction을 의미한다.
- 오른쪽에 있는 vertical line graph는 각 hypothesis의 확률을 뜻한다.
- 이 두가지의 weighted sum이 맨 위에 있는 각 숫자가 나올 확률이다.

1.5 MAP, MLE, and the puglin approximation

Figure 2.4에서 볼 수 있듯이, 데이터가 많아질수록 posterior는 한 값으로 수렴하게 되고, 이를 posterior mode라고 한다. \(h_{\textrm{map}} := \textrm{argmax}_h p(h|\mathcal{D}) \qquad{(2.19)}\)
posterior mode는 maximum posterior probability를 갖는 hypothesis로 정의되며 표현하자면 위와 같다.
이를 maximum a posterior (MAP) 라고 한다.
MAP를 optimization을 통해 구할 때, 로그를 취해도 같은 값이 얻어지기 때문에 보통 log posterior를 maximize한다.

\[h_{\textrm{map}} = \textrm{argmax}_h \log p(h|\mathcal{D}) = \textrm{argmax}_h \log p(\mathcal{D}|h) + \log p(h) \qquad{(2.20)}\]

\( \log p(\mathcal{D}|h) \)는 log likelihood 이며, \( \log p(h) \)는 log prior이다.
데이터가 independent하다는 가정하에, log likelihood term은 각 데이터에 대한 sum으로 표현될 수 있고, 따라서 데이터가 많을수록 log likelihood의 값이 dominant해진다.
- 이는 결국 prior term에 대한 의존성이 낮아진다는 것을 의미하며, 이 경우 MAP가 MLE와 동일해진다.

\[h_{\mathrm{mle}} := \textrm{argmax}_h \log p(\mathcal{D}|h) = \textrm{argmax}_h \sum_{n=1}^N \log p(y_n|h) \qquad{(2.21)}\]

posterior distribution을 point estimate한다고 가정하자. MLE에서는 당연하겠지만 MAP를 구할때는 probability distribution을 얻을 수 있는데, 그것이 충분히 하나의 점에서의 delta function에 근사한다고 가정하면

\[p(h|\mathcal{D}) \approx \mathbb{I}(h = \hat{h}) \qquad{(2.22)}\]

이를 posterior predictive distribution을 구하는 데 이용되는 Bayesian model averaging에 이용하면

\[p(y|\mathcal{D}) \approx \sum_h p(y|h) \mathbb{I}(h = \hat{h}) = p(y|\hat{h}) \qquad{(2.23)}\]

위를 plug-in approximation이라고 한다.
- 간단하기 때문에 쉽게 많이 이용되지만, distribution을 모두 고려하는 것보다는 당연히 inferior 하다.
- 이와 같이 하나의 값만을 고려하는 접근방식은 overfitting에 취약할 수 있다.
- 요새같은 딥러닝 era에서는 꼭 그렇지많은 않고, 사실 대부분의 경우에 이러한 방식을 이용하기는 한다.

2. Learning a continuous concept: the healthy levels game

지금까지는 discrete variable을 이용하는 경우에 대해서만 살펴보았다.
Continuous case에서는 sum 대신에 integral을 이용해야 하기 때문에 computation이 당연하게도 더 복잡해진다. 아래에는 예재로 healthy levels game을 이용하겠다.
- 몇 가지 parameter에 대해서, 주어진 데이터를 통해 각 parameter가 어떤 range에 있어야 healty 하다고 할 수 있는지를 예측하는 것이다.
- 여기서 예측할 값들은 insulin level과 cholesterol level이다.
Discrete case에서처럼 여기서도 hypothesis space를 제한하자.

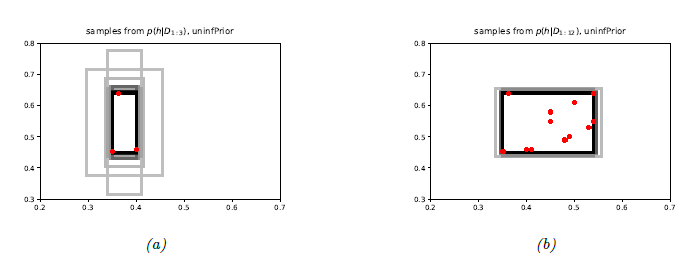
이 경우에 해당 space는 axis-parallel rectangle이 된다.
- 여기서 이러한 rectangle을 표현하기 위해 각 feature당 두 가지 파라미터를 설정한다.
  - \( \ell \): 특정 범위의 maximum value
  - \( s \): 각 feature의 range
직관적으로도, 인슐린과 콜레스테롤 수치가 특정 범위 안에 들어와야 건강하다고 할 수 있는것을 알기 때문에 이런식으로 hypothesis space를 잡는 것이 말이 된다.
위 그림의 (a)에는 positive example이 3개 주어져있다. 이 경우 uncertainty가 높은 것을 확인할 수 있다.
반면, (b)에는 훨씬 더 많은 양의 positive example이 주어져있고 따라서 uncertainty가 많이 줄어있음을 알 수 있다.

2.1 Likelihood

우선, 주어진 rectangle 안에서 positive data가 random하게 sampling되었다고 가정한다.
쉽게 생각하기 위해, 2d rectangle이 아닌 feature가 하나인 1d case를 생각해보자. 이 경우에 likelihood는 모든 positive example이 해당 interval 안에 들어있을 때만 양의 값을 갖는다.

\[p(\mathcal{D}|\ell, s) = \begin{cases} s^{-N}, & \text{if} \min (\mathcal{D}) \geq \ell \text{and} \max (\mathcal{D}) \leq \ell + s \\ 0, & \text{otherwise} \end{cases}\]

만약 두 feature가 independent 하다고 가정하면, 2d case로 쉽게 extend 가능하다.

\[p(\mathcal{D}|h = p(\mathcal{D}_1|\ell_1, s_1) p(\mathcal{D}_2|\ell_2, s_2) \qquad{(2.25)}\]

여기서 \( \mathcal{D}j = {y{nj} : n = 1 : N} \) 은 각 feature dimension에서의 observation 값의 set을 의미한다.

2.2 Prior

각 feature값들이 모두 factorization된다고 가정하면 \( p(h) = p(\ell_1)p(\ell_2)p(s_1)p(s_2) \) 로 둘 수 있다.
섹션 7.3에서 배울 uninformative prior, 다시 말해 가장 bias가 적은 prior를 이용하면, \( p(h) \propto \frac{1}{s_1} \frac{1}{s_2} \)이다.

2.3 Posterior

앞선 likelihood와 prior를 모두 합치면 다음과 같은 posterior를 얻는다.

\[p(\ell_1, \ell_2, s_1, s_2 | \mathcal{D}) \propto p(\mathcal{D}_1 | \ell_1, s_1) p(\mathcal{D}_2 | \ell_2, s_2) \frac{1}{s_1} \frac{1}{s_2} \qquad{(2.26)}\]

이를 \( \mathbb{R}^4 \) 상에서 직접 풀어볼 수도 있지만, 시각화하는 것이 매우 어렵기 때문에 좀 더 직관적으로 받아들이기 위해 posterior distribution으로부터 sampling을 하겠다.
- \( h^s \sim p(h|\mathcal{D}) \) 에서 \( h^s \)는 각각 서로 다른 위치와 크기의 rectangle들이 된다.
- 이러한 샘플된 rectangle들이 회색 박스로 그려져있는 것이 Figure 2.6에 나타나있다.

2.4 Posterior predictive distribution

앞서 discrete case에서 다룬 바와 같이, posterior predictive distribution을 구하기 위해선 각 hypothesis에 대해서 구해진 posterior를 이용해 probability를 계산하는 절차가 필요하다.
결국 구해지는 값은 어떤 data point \( \mathbf{y} \in \mathbb{R}^2 \)이 observe 될 가능성이 얼마나 높은지이다.
Posterior predictive distribution은 직접 유도해볼 수 있는데, 식을 쓸 때 편의를 위해 다음을 정의하자.
- \( y_{j}^{\textrm{min}} = \min_n y_{nj} \)
- \( y_{j}^{\textrm{max}} = \max_n y_{nj} \)
- \( d(y_j) = 0, \quad \text{if} \quad y_j^{min} \leq y_j \leq y_j^{max} \)
- \( d(y_j) \): distance to the nearest data point in dimension \( j \).
정의된 위의 notation을 이용하면 (자세한 유도과정은 연습문제 풀이에 정리해놓았다.) 아래 결과를 얻는다. \(p(\mathbf{y}|\mathcal{D}) = [\frac{1}{(1 + d(y_1)/r_1)(1 + d(y_2)/r_2)}]^{N-1} \qquad{(2.27)}\)
\( N=1 \)이면, 위 식이 의미없어지기 때문에 predictive distribution이 정의되지 않는다.
- 한 가지 data point로부터 rectangle을 infer하는 것이 의미가 없기 때문에, 직관적으로도 말이 된다.

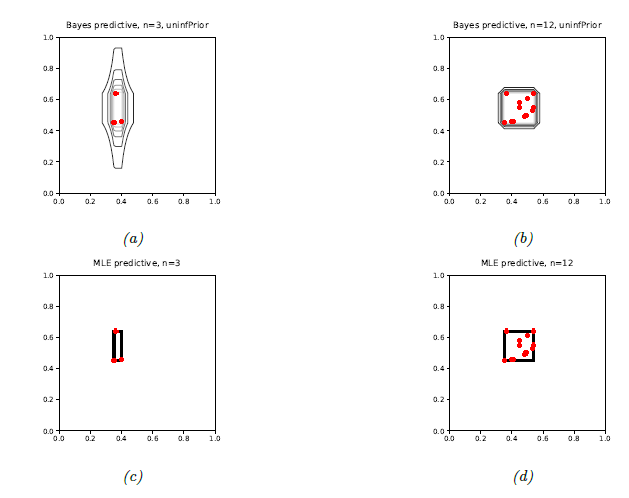
위 그림의 (a), 그리고 (b)는 posterior predictive distribution의 bayesian prediction들을 나타낸다.
- (a)를 보면 데이터가 단 3개만 주어졌을 때의 넓은 predictive distribution을 볼 수 있다.
- 데이터가 y축에서 range가 더 넓게 나타나기 때문에 예측된 rectangle들의 모양이 세로로 긴 모양임을 확인할 수 있다.
- (b)에서는 데이터가 12개일 때의 predictive distribution이며, uncertainty가 확실히 줄어든 것을 알 수 있다.
- (c), (d) 는 MLE estimate이기 때문에 data가 모두 피팅되는 가장 작은 직사각형이 선택된다.

2.5 Plug-in approximation

Posterior predictive를 구하는 원래 방법은 모든 hypothesis에 대해 integral을 취하는 것이다.

\[p(y|\mathcal{D}) = \int_h p(y|h) p(h|\mathcal{D}) \qquad{(2.18)}\]

그런데 이 방법이 computationally expensive하고 비현실적이라면 마찬가지로 plug-in approximation을 이용하는 것도 방법이다.
\( \hat{\mathbf{\theta}} \) 이 MLE/MAP estimate이라고 할 때 \( p(\mathbf{y}|\mathcal{D}) \approx p(\mathbf{y}|\hat{\mathbf{\theta}}) \) 를 바로 이용.

Chapter. 2