4. Bayesian machine learning

섹션 2.2와 2.3에서는 output으로 나오는 prediction 값 \( y \)가 input, 또는 feature에 의존하지 않았었다.
Training data는 존재하고 그로부터 \( y \)값을 예측하거나 범위를 구하는 문제들이었다.
하지만 많은 practical application에서는 특정 input \( x \)가 존재한다. 이를 input, 또는 feature라고 한다.
이 경우 training data에만 의존적인 \( p(\mathbf{y}|\mathcal{D}) \) 가 아니라 input data에까지 의존적인 \( p(\mathbf{y}|\mathbf{x}, \mathcal{D}) \) 를 구하게 된다.
이를 conditional probability distribution이라고 하고, 이 때 training data \( \mathcal{D} \) 는 전과 같이 \( \mathbf{x} \) 값만 존재하는 것이 아니라 input과 output이 pair로 존재한다.
\( \mathcal{D} = { (\mathbf{x}, \mathbf{y}) : n = 1 : N } \)로 존재하며,
- \( \mathbf{y} \)가 class label과 같은 low-dimensional data일 때 discriminative model으로 볼 수 있고,
- \( \mathbf{y} \)가 이미지와 같은 high-dimensional data일 때 conditional generative model으로 볼 수 있다.
이와 같이 prediction이 input에 dependent해지는 상황에서, 우리가 예측하고자 하는 hypothesis \( h \)는 보통 real-valued parameter \( \mathbf{\theta} \in \mathbb{R}^K \) 인 경우가 많다.
- 가장 간단한 linear regression부터 현대에 쓰이는 neural network까지 모두 이렇다.
- 이를 식으로 표현하자면 아래와 같다.

\[p(\mathbf{y}|\mathbf{x}, \mathbf{\theta}) = p(\mathbf{y}|f(\mathbf{x};\mathbf{\theta})) \qquad{(2.28)}\]

위 식에서 \( f(\mathbf{x};\mathbf{\theta}) \)는 input을 output distribution의 파라미터로 매핑시키는 역할을 한다.
결국 식 (2.28)을 완전히 표현하려면 두 가지가 필요하다.
1. Output probability distribution \( p \)
2. Form of the predictor \( f \)
일단 1번부터 알아보도록 하자.

1. Fully Bayesian approach

앞선 내용의 복습이다. Bayesian approach로 conditional predictive model을 만들기 위해선 우선 파라미터에 대한 posterior를 구한 후,

\[p(\mathbf{\theta}|\mathcal{D}) = \frac{p(\mathbf{\theta}) p(\mathcal{D}|\mathbf{\theta})}{p(\mathcal{D})} \qquad{(2.29)}\]

구해진 posterior를 이용해 posterior predictive를 계산할 수 있다.

\[p(\mathbf{y}|\mathbf{x}, \mathcal{D}) = \int p(\mathbf{y}|\mathbf{x}, \mathbf{\theta}) p(\mathbf{\theta}|\mathcal{D}) d\mathbf{\theta} \qquad{(2.30)}\]

2. Plug-in approximation

많은 경우에 posterior predictive를 위한 적분이 매우 costly할 수 있으므로, posterior를 point estimate하는 것이 더 practical할 수 있다.

MLE
- MLE를 구하기 위해선 likelihood를 최대화해야하기 때문에
\[\hat{\theta}_{\textrm{mle}} = \textrm{argmax}_\theta \log p(\mathcal{D}|\theta) = \textrm{argmin}_\theta -\frac{1}{N} \sum_{n=1}^N \log p(\mathbf{y}_n | f(\mathbf{x}_n ; \theta)) \qquad{(2.31)}\]
- log likelihood를 maximize하는 것은 negative log likelihood (NLL)을 minimze하는 것과 같고, log를 취했기 때문에 각 data에 대한 합으로 나눌 수 있다.
MAP
- MAP를 구하기 위해선 posterior를 최대화해야한다.

\[\begin{align} \hat{\theta}_{\textrm{map}} &= \textrm{argmax}_\theta \log p(\theta|\mathcal{D}) = \textrm{argmax}_\theta \log p(\mathcal{D}|\theta) + \log p(\theta) \\ &= \textrm{argmin}_\theta -[\frac{1}{N} \sum_{n=1}^N \log p(\mathbf{y}_n|f(\mathbf{x}_n;\theta))] - \log p(\theta) \end{align}\]

둘 중에 어떤 것을 이용하든, point estimate은 가져와서 그냥 이용하면 된다.

\[p(\mathbf{y}|\mathcal{D}) = \int p(\mathbf{y}|\mathbf{\theta}) p(\mathbf{\theta}|\mathcal{D}) d\mathbf{\theta} \approx \int p(\mathbf{y}|\mathbf{\theta}) \delta(\mathbf{\theta} - \hat{\mathbf{\theta}}) = p(\mathbf{y}|\hat{\mathbf{\theta}}) \qquad{(2.38)}\]

가장 쉽고 보편적인 방법이다. overfitting 될 수 있다고 하는데 딥러닝에서는 그렇지도 않다.
물론 몇 가지 plausible한 parameter를 이용하는 것은 performance도 올리고 computational burden 측면에서도 부담스럽지 않은 좋은 방법이 될 수는 있다.

3. Example: scalar input, binary output

Binary classification 예제이다. 따라서 \( y \ in {0, 1} \)이다.

\[p(y|\mathbf{x}; \mathbf{\theta}) = \textrm{Ber}(y|\sigma(\mathbf{w}^T\mathbf{x} + b)) \qquad{(2.39)}\]

여기서 \( \sigma(a) := \frac{e^a}{1 + e^a} \) 이며, 이를 sigmoid 또는 logistic function 이라고 한다.
- practical하게 많이 쓰이는 함수로, \( \mathbb{R} \mapsto [0, 1] \) 인 특성 때문에 range를 강제로 제한해야 할 때 유용하다.
- Bernoulli distribution에 대해서는 3단원에서 review한다.

위에서 정의한 logistic regression을 1d에서 풀어보자.

\[p(y = 1|x, \theta) = \sigma(b + wx) \qquad{(2.42)}\]

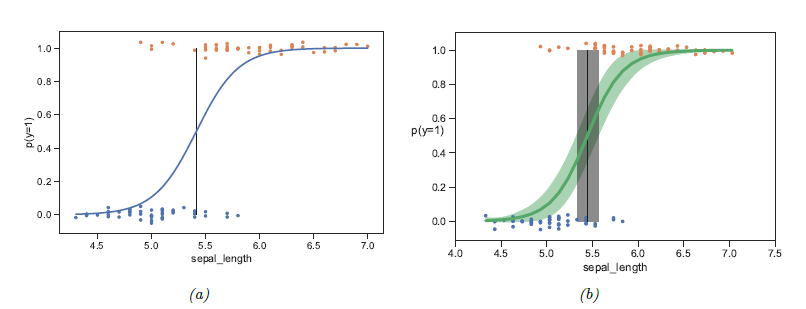
Training data를 통해 구한 MLE estimate이 \( \hat{\theta} \) 라고 하면 이를 plug-in 해서 이용할 수 있으며, 이 것이 위 그림 (a) 에 나타나있다.
Binary classification이기에 \( x \)의 어느 값을 기점으로 decision boundary를 설정할 지 정해야 하는데, 이 경계는 확률 값이 0.5인 점을 기점으로 한다.

point-estimate하지 않고 Bayesian approach를 이용하면 posterior \( p(\mathbf{\theta}

\mathcal{D}) \)를 구할 수 있고, 이러한 posterior distribution에서 \( \theta \)를 샘플링해서 이를 averaging 하는 방식도 가능하다.

\[p(y = 1|x, \mathcal{D}) \approx \frac{1}{S} \sum_{s=1}^S p(y=1|x, \mathbf{\theta^s}) \qquad{(2.46)}\]

이러한 방식으로 샘플링하고, 95% credible interval을 그림으로 표현한 것이 위 그림의 (b)에 표현되어있다.
마찬가지로 boundary를 구하는 과정에서도 posterior distribution에서 sampling하여 평균을 구할 수 있다. 이에 대한 95% confidence interval이 (b)의 회색으로 나와있다.

4. Example: binary input, scalar output

이번엔 반대의 예시이다. 택배회사 A와 B가 있고 ( \( x \in {0, 1} \) ), 이들이 물건을 배송할때 걸리는 평균 배송시간 \( y \in \mathbb{R} \)을 예측하고자 한다.
이 때는 output distribution으로 gaussian을 이용하자.

\[p(y|x, \theta) = \mathcal{N}(y|\mu_x, \sigma_x^2) \qquad{(2.48)}\]

이 때 gaussian distribution은 잘 알려진대로 다음과 같이 정의된다.

\[\mathcal{N}(y|\mu, \sigma^2) := \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{1}{2\sigma^2}(y - \mu)^2} \qquad{(2.49)}\]

위 distribution으로 각 택배회사의 평균 배송시간을 modeling하면, 각 회사별로 파라미터 값들이 정해지므로 estimate해야 하는 parameter는
- \( \mathbf{\theta} = (\mu_0, \mu_1, \sigma_0, \sigma_1) \) 이다.
- 이 파라미터 값들은 MLE, 또는 MAP 등의 방법으로 구할 수 있다. 차차 알아보도록 하자.

Bayesian approach (MAP를 estimate하는) 의 장점은 plug-in approximation처럼 한 값을 선택하는 것이 아니라 uncertainty를 함께 modeling 할 수 있다는 것이다.
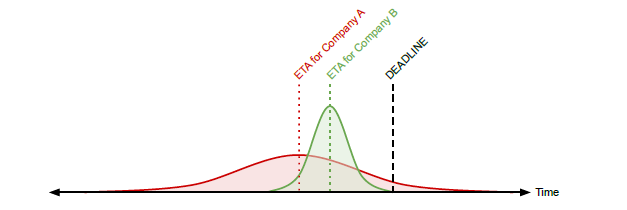
- 예를 들어 각 회사 당 하나의 observation들만 존재한다고 가정하자.
- \( \mathcal{D} = { (x_1 = 0, y_1 = 15), (x_2 = 1, y_2 = 20) } \)
- 이 경우 하나의 sample들밖에 없기 때문에 MLE를 통해 예측된 variance는 두 경우 모두 0이다.
- 실제로는 위 그림에서 볼 수 있듯이 Expected time of arrival (ETA) 에는 어느정도의 편차가 있을 것이며, 이러한 편차를 무시하게 되는 estimation은 좋지 않다는 것을 알 수 있다.

5. Scaling up

앞선 예제들은 1d input과 1d output을 이용했기 때문에 가장 간단한 형태였고, 만약 high dimensional input, high dimensional output이 involve된다면 과정이 무척 복잡해진다.

많은 경우, posterior \( p(\theta

\mathcal{D}) \) 를 계산할 수 있으면 다행이고, 현실적으로 불가능한 경우가 많다.

앞으로 책에서 나올 많은 경우에도 simplicity를 위해 plug-in approximation을 이용하게 된다.

6. Is Bayes relevant in the “big data era”?

데이터의 사이즈가 커지면서, MAP도 MLE처럼 한 점으로 집중된다.
- log posterior를 maximize하는 것이 결국 log prior + log likelihood를 maximize하는 것인데, log likelihood은 N이 커짐에 따라 계속 더해지는 데에 비해 log prior 값은 일정하기 때문이다.
그렇다면 지금과 같은 big data era에 Bayes가 irrelevant한 것은 아닐까?
이는 많은 경우에 data distribution들이 heavy tail 혹은 long tail을 갖고 있다는 것으로 반박 가능하다.
- distribution에서 각각이 높은 probability를 갖는 것은 아니지만, 이들이 관측될 확률이 작지는 않다.
- 책에 Andrew Gelman이 한 말을 인용하는데, 공감이 가기도 하고 재밌는 내용이다.
샘플 수 N이 ‘너무’ 큰 경우는 없다. N이 학습이 될만큼 ‘충분하다면’, 주어진 데이터를 나누어서 더 다양하고 많은 것들을 배울 수 있다. 또한, 만약 N이 ‘충분하다면’ 이미 당신은 데이터가 부족한 다른 문제를 풀고 있을 것이다.
Bayesian machine learning이 적용되는 또 하나의 중요한 사례는 recomender system이다.
- recomender system에서는 기존 user들의 preference를 기반으로 모델을 학습하게 되는데, 항상 새로운 user와 새로운 product가 나오기 때문에 항상 “small N” regime이 생기기 마련이다.
- Bayesian method를 이용하면 비슷한 preference를 가진 user들의 데이터를 기반으로 결과값을 쳬측할 수 있고, 이와 같이 데이터가 작은 경우에 유용하다.

7. Is Bayes relevant in the “deep learning era”?

딥러닝에서는 모델의 parameter수가 training data의 수보다 압도적으로 많다.
- 이는 prediction function \( f(\mathbf{x}; \mathbf{\theta}) \)가 underspecified 되었다는 것을 의미한다.
- Uncertainty에는 종류가 두 가지 있다.
  - Aleatoric uncertainty: 예측되는 값에 내재적으로 variance가 존재함으로 인해서 생기는 uncertainty
  - Epistemic uncertainty: 모델의 불확실성으로 인해서 생기는 uncertainty
- Bayesian method가 잘하는게 uncertainty 중 후자를 다루는 일이다.
  - 이와 관련하여 짧고 굵게 잘 정리되어있는 [article][https://arxiv.org/abs/2001.10995] 이 있다.

Chapter. 2