Chapter. 3

5. The multivariate Gaussian (normal) distribution

  • Joint probability distribution으로 가장 많이 흔히 이용되는것이 multivariate gaussian distribution 혹은 multivariate normal(MVN) distribution이다.
  • 수학적으로 다루기 편해서 그런것도 있지만, 앞선 이유들 때문에 합리적이기도 하다.
  • PRML의 2단원에 MVN에 관해 굉장히 자세히 다루는데, 정리가 잘 되어있으니 한 번 보는 것을 추천한다.

1. Definition

\[\mathcal{N}(\mathbf{y}|\boldsymbol{\mu},\mathbf{\Sigma}) := \frac{1}{(2\pi)^{D/2}|\mathbf{\Sigma}|^{1/2}} \exp \Big[ -\frac{1}{2}(\mathbf{y} - \boldsymbol{\mu})^T \mathbf{\Sigma}^{-1} (\mathbf{y} - \boldsymbol{\mu}) \Big] \qquad{(3.77)}\]
  • \( D \)-dimension일 때 위 식과 같이 정의된다.
    • \( \boldsymbol{\mu} = \mathbb{E}[\mathbf{y}] \in \mathbb{R}^D \): mean vector
    • \( \mathbf{\Sigma} = \mathrm{Cov}[\mathbf{y}] \): \( D \times D \) covariance matrix
    • 여기서 covariance matrix란 \( \mathrm{Cov}[\mathbf{y}] := \mathbb{E}\Big[ (y - \mathbb{E}[\mathbf{y}])(y - \mathbb{E}[\mathbf{y}])^T \Big]\)
\[\begin{align} \mathrm{Cov}[Y_i, Y_j] &= \mathbb{E}[(Y_i - \mathbb{E}[Y_i])(Y_j - \mathbb{E}[Y_j])]\\ &= \mathbb{E}[Y_i Y_j] - \mathbb{E}[Y_i\mathbb{E}[Y_j]] - \mathbb{E}[Y_j\mathbb{E}[Y_i]] + \mathbb{E}[Y_i]\mathbb{E}[Y_j] \end{align}\]
  • Covariance matrix의 (i, j) 번째 entry는 위와 같다.
    • 따라서 diagonal element들은 \( \mathbb{V}[Y_i] = \mathrm{Cov}[Y_i, Y_i] \) 이다.
  • Covariance matrix의 정의로부터
\[\begin{align} \mathbf{\Sigma} &= \mathbb{E}[(\mathbf{y} - \mathbb{E}[\mathbf{y}])(\mathbf{y} - \mathbb{E}[\mathbf{y}])^T]]\\ &= \mathbb{E}[\mathbf{y}\mathbf{y}^T - \boldsymbol{\mu}\mathbf{y}T - \mathbf{y}\boldsymbol{\mu}^T + \mu \mu^T]\\ &= \mathbb{E}[\mathbf{y}\mathbf{y}^T] - \boldsymbol{\mu}\boldsymbol{\mu}^T \qquad{(3.81)} \end{align}\]
  • exponential term 앞에 붙는 \( Z = (2\pi)^{D/2}|\mathbf{\Sigma}|^{1/2} \)는 normalization constant로 적분값을 1로 만들어주는 역할을 한다.
  • \( D=2 \)일 때를 bivariate gaussian이라고 하며, covariance matrix가 달라짐에 따라 서로 다른 모양을 갖는것이 아래 그림들에 표현되어있다.
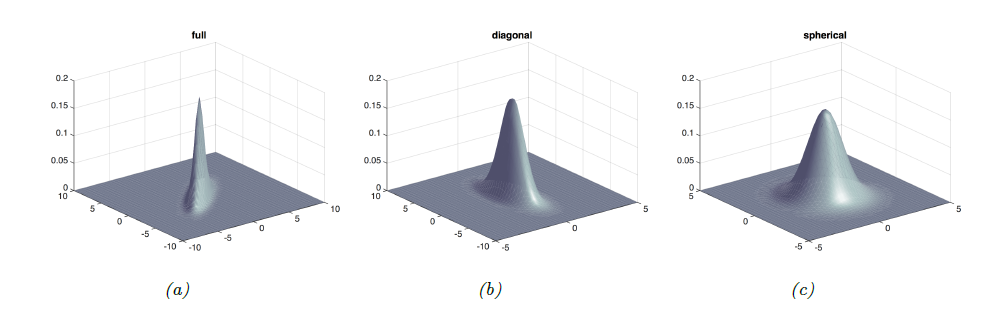
Figure 3.11
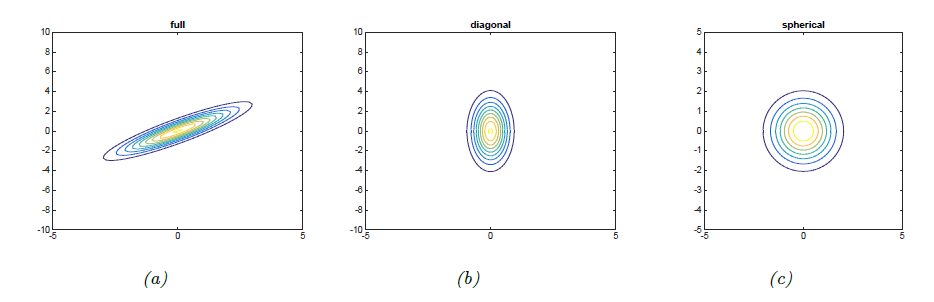
Figure 3.12
  • Covariance matrix는 정의에 따라 symmetric하므로
    • full covariance matrix는 최대 \( D(D+1)/2 \)개의 파라미터를 갖는다.
      • 이 경우에 가장 자유도가 높으므로 자유분방하게 생긴(?) 타원 level set을 생각할 수 있다.
      • 3.11과 3.12의 (a)
    • Diagonal covariance matrix는 \( Cov[Y_i, Y_j] = 0 \, i \neq j \)인 경우이며 D개의 파라미터 값을 갖는다.
      • Diagonal matrix가 형성되며, 각 axis에 수직한 타원 level set을 갖는다.
      • 3.11과 3.12의 (b)
    • Isotropic covariance matrix는 variance값으로 scale된 identity matrix.
      • 3.11과 3.12의 (c)

2. Mahalanobis distance

  • Normalization constant \( Z \)를 제외하면 결국 gaussian은 exponential function의 형태를 띈다.
  • 이를 다루기 편하게 하기 위해 log를 취하고 지수 부분만을 보는 경우가 많은데,
\[\log p(\mathbf{y}|\boldsymbol{\mu}, \mathbf{\Sigma}) = -\frac{1}{2}(\mathbf{y} - \boldsymbol{\mu}^T)\mathbf{\Sigma}^{-1}(\mathbf{y} - \boldsymbol{\mu}) + \mathrm{(const)} \qquad{(3.85)}\]
  • 위 식과 같이 주어진다. 여기서 Mahalanobis distance를 아래와 같이 정의한다.
\[\Delta^2 := (\mathbf{y} - \boldsymbol{\mu})^T \mathbf{\Sigma}^{-1} (\mathbf{y} - \boldsymbol{\mu}) \qquad{(3.86)}\]
  • 그림 3.12에서 보았던 level set을 생각해보면, 같은 level set은 결국 같은 \( \Delta \) 값을 갖는 것으로 생각할 수 있다.
  • Covariance 값은 non-negative이고, 따라서 positive semi-definite (PSD) matrix이다.
    • 책에는 positive definite이라고 나와있고 full rank를 가정하는 것 같은데, 중요한 컨셉은 그게 아니니 넘어가자.
  • Symmetric PSD matrix는 해당 matrix나 그 matrix의 inverse인 \(\mathbf{\Lambda} = \mathbf{\Sigma}^{-1} \) 모두 diagonalizable 하다.
  • 따라서 이를 eigendecomposition해서 표현하면
\[\mathbf{\Sigma} = \sum_{d=1}^D \lambda_d \mathbf{u}_d \mathbf{u}_d^T \qquad{(3.87)}\] \[\mathbf{\Sigma}^{-1} = \sum_{d=1}^D \frac{1}{\lambda_d} \mathbf{u}_d \mathbf{u}_d^T \qquad{(3.88)}\]

-이렇게 eigenvector와 eigenvalue로 Mahalanobis distance를 표현하고, 추가적으로 \( z_d := \mathbf{u}_d^T (\mathbf{y} - \boldsymbol{\mu})\), 따라서 \( \mathbf{z} = \mathbf{U}(\mathbf{y} - \boldsymbol{\mu}) \)를 이용하면,

\[\begin{align} \Delta^2 &= (\mathbf{y} - \boldsymbol{\mu})^T (\sum_{d=1}^D \frac{1}{\lambda_d} \mathbf{u}_d \mathbf{u}_d^T) (\mathbf{y} - \boldsymbol{\mu}) \\ &= \sum_{d=1}^D \frac{1}{\lambda_d}(\mathbf{y} - \boldsymbol{\mu})^T \mathbf{u}_d \mathbf{u}_d^T (\mathbf{y} - \boldsymbol{\mu}) = \sum_{d=1}^D \frac{z_d^2}{\lambda_d} \end{align}\]
  • 이렇게 식을 바꿔서 해석해보면, 결국 Mahalanobis distance가 같다는 것은 새로운 좌표계인 \( \mathbf{z} \) 좌표계에서 Euclidean distance가 같다는 것을 의미한다.
    • 그리고 이 새로운 좌표계는 \( \mathbf{y} \)를 rotation matrix \( \mathbf{U} \)로 돌리고 \( \mathbf{\Lambda} \)로 scale해서 얻어진다. -2-d case로 예를 들자면 \(\frac{z_1^2}{\lambda_1} + \frac{z_2^2}{\lambda_2} = r \qquad{(3.91)}\)
  • 위에 있는 점들은 모두 같은 Mahalanobis distance를 갖는데, 이 모양은 타원의 형태를 띄므로 Figure 3.12의 level set들이 타원 모양을 가졌던 것이다.
  • PSD matrix는 스칼라 값의 scalar 값을 구하듯이 \( L^T L \)와 같이 factorization도 가능한데, \( \mathbf{\Sigma}^{-1} = \mathbf{L}^T \mathbf{L} \)을 정의하자.
    • 이 때 \( \mathbf{L}: \mathbb{R}^D \mapsto \mathbb{R}^d, \quad d \leq D \) 이며, mahalanobis distance를 \( \boldsymbol{\delta} = \mathbf{y} - \boldsymbol{\mu} \)를 이용해 전개해보면
\[\Delta^2 = \| \mathbf{L} \boldsymbol{\delta} \|^2_2 \qquad{(3.92)}\]
  • 위 식을 얻는다. 따라서 \( D \) 보다 작은 dimension인 \( d \) dimension에서의 Euclidean distance로도 생각할 수 있다.

3. Marginals and conditionals of an MVN

  • 이제 MVN의 marginal/conditional distribution을 알아볼 것인데, 직접 계산하면서 알아보기 위해 2D discrete case with random variables \( Y_1, Y_2 \) 인 경우를 생각하자.
\( p(Y_1, Y_2) \) \( Y_1 = 0 \) \( Y_2 = 1 \)
\( Y_1 = 0 \) 0.2 0.3
\( Y_2 = 1 \) 0.3 0.2
  • \( Y_1, Y_2 \)의 joint distribution이 있을 때 marginal distribution은 다음과 같다.
\[p(Y_2 = y_2) = \sum_{y_1}p(Y_1 = y_1, Y_2 = y_2) \qquad{(3.93)}\]
  • conditional distribution은 아래와 같이 정의된다.
\[p(Y_1 = y_1 | Y_2 = y_2) = \frac{p(Y_1 = y_1, Y_2 = y_2)}{p(Y_2 = y_2)} \qquad{(3.94)}\]
  • 위 결과를 jointly Gaussian random variable에 대해 확장시켜보자.
    • \( \mathbf{y}_2 \)가 variable of interest일 때 \( \mathbf{y}_1 \)은 nuisance variable이라고 부른다.
    • 이 nuisance variable을 marginalize out 해보자
\[p(\mathbf{y}_2) = \int \mathcal{N} (\mathbf{y}| \boldsymbol{\mu}, \Sigma)\,d\mathbf{y}_1 = \mathcal{N}(\mathbf{y}_2|\boldsymbol{\mu}_2, \mathbf{\Sigma}_{22}) \qquad{(3.95)}\]
  • 위 식에서 이용된 mean과 covariance matrix는 아래와 같다.
\[\boldsymbol{\mu} = \begin{pmatrix}\boldsymbol{\mu}_1 \\ \boldsymbol{\mu}_2\end{pmatrix}\, , \, \mathbf{\Sigma} = \begin{pmatrix} \mathbf{\Sigma}_{11} & \mathbf{\Sigma}_{12} \\ \mathbf{\Sigma}_{21} & \mathbf{\Sigma}_{22} \end{pmatrix} \qquad{(3.96)}\]
  • 이제 만약 \( \mathbf{y}_2 \)를 observe하고, 이를 통해 \( \mathbf{y}_1 \)의 값을 예측하고 싶다고 하자.
  • 이는 결국 posterior인 \( p(\mathbf{y}_1 | \mathbf{y}_2) \)를 예측하는 문제가 되며, 이를 계산해보면 아래와 같은 식이 나온다.
\[p(\mathbf{y}_1 | \mathbf{y}_2) = \mathcal{N}(\mathbf{y}_1|\boldsymbol{\mu}_1 + \mathbf{\Sigma}_{12} \mathbf{\Sigma}_{22}^{-1}(\mathbf{y}_2 - \boldsymbol{\mu}_2), \, \mathbf{\Sigma}_{11} - \mathbf{\Sigma}_{12}\mathbf{\Sigma}_{22}^{-1}\mathbf{\Sigma}_{21}) \qquad{(3.94)}\]
  • 증명이 좀 복잡한 편인데, 따로 정리해놓았다. proof
  • 위 식의 mean과 variance를 살표보자
    • mean: \( \mathbf{y}_2 \)에 대한 linear function이다.
    • variance: \( \mathbf{y}_2 \)에 independent하다. 기존 covariance에만 영향을 받는다는 것을 알 수 있다.

4. Example: Imputing missing values

  • 이번 예제는 \( \mathbf{y} \) 벡터의 일부분 (일부 dimension)만 observe했다고 가정하고, 나머지 missing dimension을 covarinace matrix로부터 유추하는 과정을담는다.
    • 이를 missing value imputation이라고 한다.
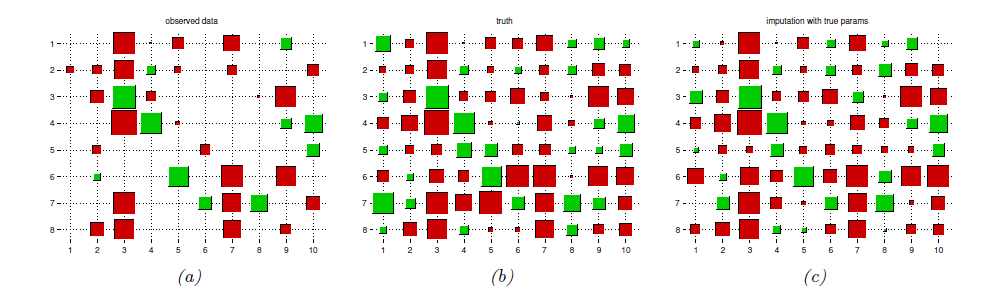
Figure 3.13
  • 위 그림은 MVN을 이용한 missing data imputation의 한 예시이다.
    • 빨간색이 클수록 +쪽으로 크고, 초록색이 클수록 -쪽으로 크다.
    • 이런 식의 visualization을 Hinton diagram이라고 한다.
    • (c)는 posterior distribution을 계산해 mean 값을 나타낸 diagram이다. (a)에 있던 데이터만 갖고 유추한 것 치고는 ground truth인 (b)에 가까운 것을 볼 수 있다.
  • 먼저, \( N = 8 \)개의 \( D = 10 \)dimensional vector를 Gaussian에서 sampling 한 후, 각 vector의 50%를 지워버린다.
  • 그 후에, 우리가 알고있는 true model parameter로부터 비는 값을 예측한다.
    • 물론 실제로는 이 true parameter 라는 값도 당연히 유추해야겠지만, 예제이므로 알고 있다고 가정한다.
  • 결국 아래 식을 유추하는 문제가 된다.
\[p(\mathbf{y}_{n, \mathbf{h}} | \mathbf{y}_{n, \mathbf{v}}, \boldsymbol{\theta})\]
  • parameter는 다음과 같이 정리된다.
    • \( n \): Data matrix의 각 row
    • \( \mathbf{v} \): 해당 row의 visible entry
    • \( \mathbf{h} \): 나머지 보이지 않는 entry
    • \( \boldsymbol{\theta} = (\boldsymbol{\theta}, \boldsymbol{\Sigma}) \): 모델의 true parameter
  • 이 파라미터 값들을 이용해서, 각 missing variable \(i \in \mathbf{h} \)를 marginal distribution \( p(y_{n, i}| \mathbf{y}_{n, \mathbf{v}}, \boldsymbol{\theta}) \)을 구해서 얻을 수 있으며
  • 구해진 marginal distribution의 mean 값을 통해 빈 값을 채운다.
  • 물론, 이와 같이 mean으로 채우는 이유는 mean 값이 squared error의 expected value를 minimize하는 값이라서 그렇지만, 실제로는 이 유추된 값 또한 distribution의 한 샘플이기 때문에, Variance를 고려하여 여러 개 sampling하는 방식도 있다.
    • 이를 multiple imputation이라고 한다.
    • 이 것이 가능한 경우에는 당연하게도 더 robust한 방법이다.
  • 깃헙에 코드가 올라와있긴 한데 오래된 코드라 그런지 이용된 함수들이 matlab에서 돌아가지 않는다.. 혹시 방법을 아시는 분이 있으면 댓글 달아주시길 부탁드립니다 :)