- 바로 전 섹션에서 Gaussian random vector의 빈 부분을 채우는 방법을 공부했다.
- 이제 그것을 넘어, noisy observation이 있는 경우 어떻게 해야 하는 지를 알아보자.
- 우선, \( \mathbf{z} \in \mathbb{R}^D \)가 unknown vector value이고, \( \mathbf{y} \in \mathbb{R}^K \) 가 noisy observation이라고 가정하자.
- 위와 같이 \( \mathbf{y} \)는 \( \mathbf{z} \) 에 dependent하며, \( \mathbf{W} \in \mathbb{R}^{D \times K}\)matrix를 통해 관계식이 정립된다.
- \( p(\mathbf{z}, \mathbf{y}) = p(\mathbf{z})p(\mathbf{y}|\mathbf{z}) \)의 joint distribution의 평균과 분산은 아래와 같이 정의되며, 증명은 따로 정리해두었다. proof
- 마찬가지로, Bayes rule을 이용해서 posterior \( p(\mathbf{z}|\mathbf{y}) \)에 대한 parameter 값도 analytic하게 구할 수 있으며, 위 증명에 같이 정리되어있다.
- 이를 Bayes’ rule for Gaussians 라고 한다.
- 마찬가지로, normalization constant \( p(\mathbf{y}) \)도 Gaussian의 형태로 정리가 되며, 따라서 prior, posterior, marginal 모두 Gaussian이라는 것을 알 수 있다.
Gaussian prior 과 Gaussian likelihood가 합해지면 Gaussian posterior를 얻을 수 있고, 이와 같이 같은 형태의 likelihood/posterior를 얻을 수 있게 해주는 likelihood를 conjugate prior라고 한다.
1. Example: inferring a latent vector from a noisy sensor
- 우리가 알고자 하는 벡터 \( \mathbf{z} \in \mathbb{R}^D \)가 있다고 하자.
- 이에 대한 prior는 Gaussian prior \( p(\mathbf{z}) = \mathcal{N}(\boldsymbol{\mu}_z, \boldsymbol{\Sigma}_z) \)로 주어진다.
- 만약 아는게 아무것도 없다면, \( \boldsymbol{\Sigma}_z = \infty \mathbf{I} \)로 설정하는 것이 합리적일 것이다.
- 아는게 아무것도 없으므로, 평균 또한 0으로 두자.
- \( \mathbf{z} \)에 대한 noisy observation \( \mathbf{y}_n \)을 N번 샘플링 했다고 생각하자. (dimension K는 오타인듯..?) \(p(\mathcal{D}|\mathbf{z}) = \prod_{n=1}^{N} \mathcal{N}(\mathbf{y}_n|\mathbf{z}, \boldsymbol{\Sigma}_y) = \mathcal{N}(\bar{\mathbf{y}}|\mathbf{z}, \frac{1}{N}\boldsymbol{\Sigma}_y) \qquad{(3.40)}\)
- 위 식을 정리할 때 \( N \) 개의 observation 평균 \( \bar{\mathbf{y}} \)을 이용하여 대체했고, 그에 맞게 covariance matrix를 \( N \)으로 나누어주는 trick을 이용했다.
- 여기서 \( \mathbf{W} = \mathbf{I}, \mathbf{b} = \mathbf{0} \)를 적용하면, 위에서 정리한 Bayes rule for Gaussian 식을 그대로 적용할 수 있고, posterior distribution \( p(\mathbf{z}|\mathcal{D}) \)를 얻을 수 있다.

- 위 그림은 이러한 linear Gaussian system의 2D 예제를 보여준다.
- \( \mathbf{z} \): 2d 공간의 좌표
- \( \mathbf{y}_n \): 좌표의 noisy observation
- \( \mathbf{y}_n \)을 더 많이 관측할수록, 실제 값 \( \mathbf{z} \)을 더 쉽게 유추할 수 있게 된다.
- 이를 temporal axis로까지 연장한 알고리즘을 Kalman filter 알고리즘이라고 한다.
- 위 그림의 맨 오른쪽을 보면 posterior distribution이 어떻게 형성되었는지를 볼 수 있다. \( \mathbf{z} \)의 각 좌표 중 더 많이 퍼진 horizontal axis가 uncertainty가 더 높고, 따라서 해당 sensor에 대한 reliability가 떨어진다고 해석할 수 있다.
2. Example: inferring a latent vector from multiple noisy sensors
- 이제 바로 앞선 섹션에서 풀었던 noisy sensor문제를 sensor가 여러개 인 상황에서 가정해보자.
- 파라미터들은 다음과 같이 정의된다.
- \( M \): 센서의 갯수
- \( N_m \): 센서 \( m \)에서 observation의 갯수
- 따라서, M개의 서로 다른 센서에서 얻은 N개의 observation들로 posterior \( p(\mathbf{z}|\mathbf{y}) \)를 추론해내는 것이 우리의 목표이다.
- \( \mathbf{y}_1 \sim \mathcal{N}(\mathbf{z},\boldsymbol{\Sigma}_1) \)
- \( \mathbf{y}_2 \sim \mathcal{N}(\mathbf{z},\boldsymbol{\Sigma}_2) \)
- 위와 같은 두 센서로부터 데이터를 얻게 되며, 이를 concatenation해서 하나의 벡터 \( \mathbf{y} = [\mathbf{y}_1, \mathbf{y}_2] \)로 나타낼 수 있다.
- \( p(\mathbf{y}|\mathbf{z}) = \mathcal{N}(\mathbf{y}|\mathbf{W}\mathbf{z}, \boldsymbol{\Sigma}_y) \)와 같은 형태로 likelihood를 표현할 수 있게 되는데, 이 때
- \( \mathbf{W} = [\mathbf{I}; \mathbf{I}] \)
- \( \boldsymbol{\Sigma}_y = [\boldsymbol{\Sigma}_1, \mathbf{0}; \mathbf{0}, \boldsymbol{\Sigma}_2]) \)
- 이제 식 (3.103)과 식 (3.104)를 바로 이용해 posterior를 구할 수 있다.
- 일단 \( \boldsymbol{\Sigma}_1 = \boldsymbol{\Sigma}_2 = 0.01 \mathbf{I} \) 인 경우를 예로 들어보자.
- 추가적인 assumption으로, \( \boldsymbol{\Sigma}_z = 0.01 \mathbf{I} \)도 가정하자.
- 아래와 같은 결과를 얻는다.
- 결국 분산값은 각 sensor에 대해 얼마나 신뢰도가 있었는지에 따라 additive하게 증가하게 되고, 평균값은 각 sensor 평균을 신뢰도에 따라 weighted sum을 한 결과가 나오게 된다.
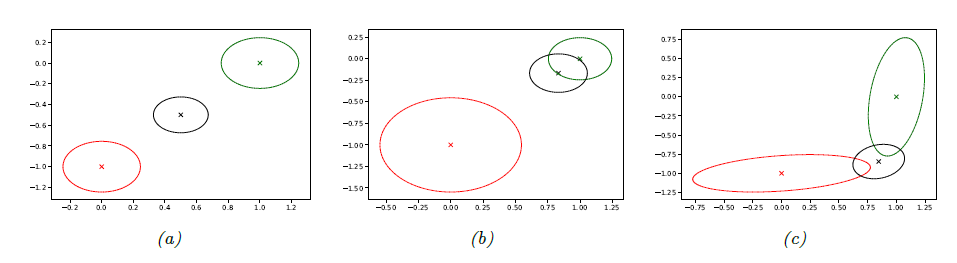
- 위 그림의 (a)가 위에 든 예시의 경우이다.
- (b)는 \( \boldsymbol{\Sigma}_1 = 0.05\mathbf{I}_2, \boldsymbol{\Sigma}_2 = 0.01 \mathbf{I}_2 \)로 sensor 2가 sensor1보다 분산이 낮고 더 reliable한 경우로, 평균이 sensor2의 평균쪽으로 더 치우치게 된다.
- (c)에서는 아래를 가정해, 각 dimension에 대한 신뢰도를 다르게 설정한 경우이다. \(\boldsymbol{\Sigma}_1 = 0.01\begin{pmatrix}10 & 1 \\ 1 & 1\end{pmatrix}\, , \, \boldsymbol{\Sigma}_2 = 0.01\begin{pmatrix}1 & 1 \\ 1 & 10\end{pmatrix} \qquad{(3.45)}\)