Chapter. 3

7. Mixture models

  • 복잡한 probiability model을 만드는 가장 단순한 방법은, 간단한 probability distribution들의 convex combination을 이용하는 것이다.
  • convex combination이란 비율의 합이 1이어야 한다는 의미이고, 식을 아래와 같이 표현할 수 있다.
\[p(\mathbf{y}|\boldsymbol{\theta}) = \sum_{k=1}^K \pi_k p_k(\mathbf{y}) \qquad{(3.112)}\]
  • 위와 같은 모델을 hierarchical model로 표현하기 위해 새로운 latent variable \( z \in {1, \dots, K} \)를 이용한다.
    • 이 latent variable은 output \( \mathbf{y} \)를 위해 어떤 distribution을 이용할 지를 결정한다.
    • 이 latent variable에 대한 prior는 \( p(z = k) = \pi_k \)이고,
    • conditional distribution은 \( p(\mathbf{y}|z = k) = p_k(\mathbf{y}) = p(\mathbf{y}|\boldsymbol{\theta}_k)\)로 정해진다.
    • 정리하자면 아래와 같다.
\[\begin{align} p(z|\boldsymbol{\theta}) &= \textrm{Cat}(z|\boldsymbol{\pi}) \qquad{(3.113)} \\ p(\mathbf{y}|z = k, \boldsymbol{\theta}) &= p(\mathbf{y}|\boldsymbol{\theta}_k) \qquad{(3.114)} \end{align}\]
  • 풀어서 생각해보면, 우선 latent variable인\( z\)를 categorical distribution으로부터 하나 샘플하고, 이에 conditioning된 \( \mathbf{y} \)를 순차적으로 얻는 식으로 진행된다.
  • 여기서 \( z \)를 marginalize 해보면
\[p(\mathbf{y}|\boldsymbol{\theta}) = \sum_{k=1}^K p(z=k|\boldsymbol{\theta})p(\mathbf{y}|z=k,\boldsymbol{\theta}) = \sum_{k=1}^K \pi_k p(\mathbf{y}|\boldsymbol{\theta}_k) \qquad{(3.115)}\]
  • 결국 식 3.112와 같은 것을 알 수 있다.
  • Mixture model의 building block이 되는 \( p() \) distribution을 무엇으로 결정하냐에 따라서 mixture model도 많이 달라지게 된다. 그 예시를 살펴보자.

1. Gaussian mixture models

  • 가장 많이 이용되는 mixture model일 것이다.
    • Gausian mixture model (GMM) 혹은 mixture of Gaussians (MoG)라고 불린다.
\[p(\mathbf{y}) = \sum_{k=1}^K \pi_k \mathcal{N}(\mathbf{y}|\boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k) \qquad{(3.116)}\]
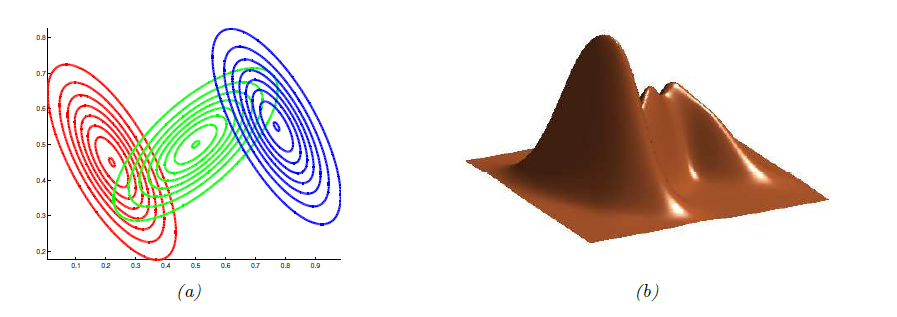
Figure 3.16
  • 위 그림은 3개의 superposition으로 구성된 2D에서의 GMM을 보여주고 있다.
  • 이 갯수를 충분히 크게 만들면, GMM으로 \( \mathbb{R}^D \)의 어떠한 smooth distribution도 근사할 수 있다.

1.1 Using GMMs for clustering

  • GMM이 많이 쓰이는 분야는 unsupervised clustering이다.
  • clustering이 진행되는 방식은 아래와 같다.
    1. MLE \( \hat{\boldsymbol{\theta}} = \text{argmax} \log p(\mathcal{D}|\boldsymbol{\theta}) \)를 구한다.
    2. 각 data point \( \mathbf{y}_n \)에 그것이 해당하는 latent variable \( z_n \in {1, \dots, K} \)를 매칭시킨다.
  • 1번을 어떻게 하는지는 뒤에 나올 섹션들에서 알아보자.
  • 2번은 결국 각 data point가 어느 cluster에 속하는지를 알아내는 과정인데, 이를 responsitiblity라고 하고 posterior distribution을 formal하게 정의할 수 있다.
\[r_{nk} := p(z_n = k|\mathbf{y}_n, \boldsymbol{\theta}) = \frac{p(z_n=k|\boldsymbol{\theta})p(\mathbf{x}_n|z_n = k, \boldsymbol{\theta})}{\sum_{k'=1}^K p(z_n = k'|\boldsymbol{\theta})p(\mathbf{y}_n|z_n = k', \boldsymbol{\theta})} \qquad{(3.51)}\]
  • \( r_{nk} \)
    • \( n \): data point n
    • \( k \): cluster k
  • 여기서 cluster \( k \)에 대한 MLE를 계산하면
\[\hat{z}_n = \text{arg} \max_k r_{nk} = \text{arg} \max_k [\log p(\mathbf{y}_n|z_n = k, \boldsymbol{\theta}) + \log p(z_n = k|\boldsymbol{\theta})] \qquad{(3.118)}\]
  • 위와 같은 방식을 hard clustering이라고 하고, 각 데이터 포인트에 확률적으로 다른 cluster class를 assign하는 방식을 soft clustering이라고 한다.
  • \( z_n \)에 uniform prior를 부여하여 모든 cluster에 같은 확률을 부여하고, \( k \)번째 Gaussian의 파라미터를 각각 \( \hat{\boldsymbol{\mu}_k}, \boldsymbol{\Sigma}_k = \mathbf{I} \)라고 하면, 결국 각 cluster의 평균점과의 mse를 minimize하는 문제가 된다.
\[z_n = \text{arg}\min_k \|\mathbf{y}_n - \hat{\boldsymbol{\mu}}_k\|_2^2\]
  • 이는 K-means clustering algorithm의 기본이 된다.

1.2 Using GMMs as a prior to regularize an inverse problem

\(\mathbf{y} = \mathbf{W}\mathbf{z} + \sigma^2 \mathbf{I}\)

  • 위와 같은 흔한 inverse problem을 생각해보자.
    • 이 때 noise가 white gaussian이라는 assumption이 들어갔는데, 이는 흔히 이용되는 가정이다.
    • \( \mathbf{W} \)는 일반적으로 forward opeartor라고 하며, denoising일 시 identity matrix, deblurring(deconvolution)일 시 특정 사이즈의 blur kernel 등이 된다.
  • 이를 likelihood로 표현하면 아래와 같다.
\[p(\mathbf{y}|\mathbf{z}) = \mathcal{N}(\mathbf{y}|\mathbf{W}\mathbf{z}, \sigma^2 \mathbf{I}) \qquad{(3.120)}\]
  • 결국 inverse problem을 구하는 문제는 MAP estimate \( \hat{\mathbf{z}} = \text{argmax}p(\mathbf{z} \mathbf{y}) \)을 구하는 문제로도 표현이 될 수 있다.
  • 다만, inverse problem의 특성 상 무수히 많은 (서로 다른) \( \mathbf{z} \)가 같은 \( \mathbf{y} \)로 매핑될 수 있기 때문에 solution space를 제한하기 위해 regularization이 필수적이다.
  • \( \mathbf{z} \)에 대한 prior로 GMM을 사용한다면, \( p(\mathbf(z)) = \sum_{k=1}^K p(c=k)\mathcal{N}(\mathbf{z} \boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k) \)로 표현할 수 있고, joint distribution은 아래와 같이 표현 가능하다.
\[\begin{align} p(\mathbf{y}, \mathbf{z}) &= p(\mathbf{z})p(\mathbf{y}|\mathbf{z})\\ &= p(c=k)\mathcal{N}(\mathbf{z}|\boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k)\mathcal{N}(\mathbf{y}|\mathbf{W}\mathbf{z}, \sigma^2 \mathbf{I})\]